The data set used in this section is gum.dat from Silagy (2003).
The do-file is gum.do.
The programs used are gllamm and gllapred. Use the command ssc describe gllamm and follow instructions to download these GLLAMM commands. For more information on GLLAMM see http://www.gllamm.org.
Read and list data:
insheet using gum.dat, clear
rename study studynam
gen study=_n
list, clean
studynam d1 n1 d0 n0 study
1. Blondal 1989 37 92 24 90 1
2. Campbell 1991 21 107 21 105 2
3. Fagerstrom 1982 30 50 23 50 3
4. Fee 1982 23 180 15 172 4
5. Garcia 1989 21 68 5 38 5
6. Garvey 2000 75 405 17 203 6
7. Gross 1995 37 131 6 46 7
8. Hall 1985 18 41 10 36 8
9. Hall 1987 30 71 14 68 9
10. Hall 1996 24 98 28 103 10
11. Hjalmarson 1984 31 106 16 100 11
12. Huber 1988 31 54 11 60 12
13. Jarvis 1982 22 58 9 58 13
14. Jensen 1991 90 211 28 82 14
15. Killen 1984 16 44 6 20 15
16. Killen 1990 129 600 112 617 16
17. Malcolm 1980 6 73 3 121 17
18. McGovern 1992 51 146 40 127 18
19. Nakamura 1990 13 30 5 30 19
20. Niaura 1994 5 84 4 89 20
21. Niaura 1999 1 31 2 31 21
22. Pirie 1992 75 206 50 211 22
23. Puska 1979 29 116 21 113 23
24. Schneider 1985 9 30 6 30 24
25. Tonnesen 1988 23 60 12 53 25
26. Villa 1999 11 21 10 26 26
27. Zelman 1992 23 58 18 58 27
Prepare data for analysis, creating variables
gum=1 if in treatment arm, 0 otherwise
quit=1 if quit smoking, 0 otherwise
wt1: frequency weight
reshape long d n, i(study) j(gum)
(note: j = 0 1)
Data wide -> long
-----------------------------------------------------------------------------
Number of obs. 27 -> 54
Number of variables 6 -> 5
j variable (2 values) -> gum
xij variables:
d0 d1 -> d
n0 n1 -> n
-----------------------------------------------------------------------------
gen y0 = n-d
rename d y1
gen i=_n
reshape long y, i(i) j(quit)
(note: j = 0 1)
Data wide -> long
-----------------------------------------------------------------------------
Number of obs. 54 -> 108
Number of variables 7 -> 7
j variable (2 values) -> quit
xij variables:
y0 y1 -> y
-----------------------------------------------------------------------------
drop i
rename y wt1
sort study gum quit
list in 1/12, clean
quit study gum studynam wt1 n
1. 0 1 0 Blondal 1989 66 90
2. 1 1 0 Blondal 1989 24 90
3. 0 1 1 Blondal 1989 55 92
4. 1 1 1 Blondal 1989 37 92
5. 0 2 0 Campbell 1991 84 105
6. 1 2 0 Campbell 1991 21 105
7. 0 2 1 Campbell 1991 86 107
8. 1 2 1 Campbell 1991 21 107
9. 0 3 0 Fagerstrom 1982 27 50
10. 1 3 0 Fagerstrom 1982 23 50
11. 0 3 1 Fagerstrom 1982 20 50
12. 1 3 1 Fagerstrom 1982 30 50
Continuous random intercept and slope model for Table 9.9 using gllamm (iteration log not shown):
gen treat = gum -0.5
gen cons=1
eq int: cons
eq slop: treat
gllamm quit treat, i(study) nrf(2) eqs(int slop) l(logit) /*
*/ f(binom) weight(wt) adapt nocor trace allc
number of level 1 units = 5908
number of level 2 units = 27
Condition Number = 1.7685027
gllamm model
log likelihood = -3074.1459
------------------------------------------------------------------------------
quit | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
treat | .5670943 .0881729 6.43 0.000 .3942786 .73991
_cons | -1.1658 .1401855 -8.32 0.000 -1.440559 -.8910418
------------------------------------------------------------------------------
Variances and covariances of random effects
------------------------------------------------------------------------------
***level 2 (study)
var(1): .48050074 (.15333759)
cov(2,1): fixed at 0
var(2): .05190697 (.04639595)
------------------------------------------------------------------------------
------------------------------------------------------------------------------
quit | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
quit |
treat | .5670943 .0881729 6.43 0.000 .3942786 .73991
_cons | -1.1658 .1401855 -8.32 0.000 -1.440559 -.8910418
-------------+----------------------------------------------------------------
stu1_1 |
cons | .6931816 .1106042 6.27 0.000 .4764014 .9099619
-------------+----------------------------------------------------------------
stu1_2 |
treat | .227831 .101821 2.24 0.025 .0282656 .4273964
------------------------------------------------------------------------------
Slight discrepancy for the treatment effect standard deviation disappears when nip(20) is used.
Empirical Bayes predictions of study-specific effect sizes using gllapred:
gllapred eff, u (means and standard deviations will be stored in effm1 effs1 effm2 effs2) Non-adaptive log-likelihood: -3078.3785 -3101.5793 -3092.8436 -3088.3938 -3084.9338 -3081.8962 -3079.2417 -3077.5891 -3076.3852 -3074.9084 -3074.1634 -3074.1459 -3074.1459 log-likelihood:-3074.1459
95% intervals
gen eff = effm2 + _b[treat] gen lower = effm2 + _b[treat] - 1.96*effs2 gen upper = effm2 + _b[treat] + 1.96*effs2
List results:
sort study
qui by study: gen last=_n==_N
list studynam lower eff upper if last==1, clean
studynam lower eff upper
4. Blondal 1989 .222363 .5866519 .9509408
8. Campbell 1991 .0146321 .3882984 .7619646
12. Fagerstrom 1982 .1783771 .5678892 .9574013
16. Fee 1982 .1462535 .5193934 .8925332
20. Garcia 1989 .2424062 .6489648 1.055523
24. Garvey 2000 .3575259 .6972256 1.036925
28. Gross 1995 .2477593 .6437063 1.039653
32. Hall 1985 .19287 .5980018 1.003134
36. Hall 1987 .3139485 .6961169 1.078285
40. Hall 1996 -.0332232 .3325011 .6982254
44. Hjalmarson 1984 .259717 .6314499 1.003183
48. Huber 1988 .4692236 .8577137 1.246204
52. Jarvis 1982 .3085245 .7037886 1.099053
56. Jensen 1991 .1502759 .4940711 .8378663
60. Killen 1984 .1223252 .5393925 .9564598
64. Killen 1990 .0739083 .3133026 .5526969
68. Malcolm 1980 .2148292 .6320365 1.049244
72. McGovern 1992 .0535688 .3903244 .7270799
76. Nakamura 1990 .2542217 .6702684 1.086315
80. Niaura 1994 .1086343 .5270553 .9454764
84. Niaura 1999 .0755295 .5087444 .9419592
88. Pirie 1992 .2841303 .5926718 .9012133
92. Puska 1979 .139473 .5054876 .871502
96. Schneider 1985 .1465653 .5650316 .983498
100. Tonnesen 1988 .2204977 .6133725 1.006247
104. Villa 1999 .1476256 .5656016 .9835777
108. Zelman 1992 .1351462 .522485 .9098238
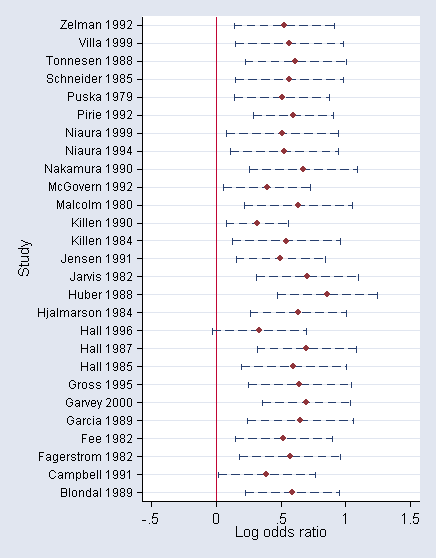
Plot results using forest plot (similar to Figure 9.6):
encode studynam, gen(s) twoway (rcap lower upper s, horizontal blpattern(dash)) (scatter s eff), /* */ ylabel(1(1)27,valuelabels angle(horizontal) labs(small)) legend(off) /* */ xscale(range(-.5 1.5)) ysize(7) xlab(-.5(.5)1.5) xline(0) saving(gumf)
Nonoarametric maximum likelihood (NPML) estimates using gateaux derivative:
Start with two masses (iteration log not shown):
gllamm quit treat, i(study) nrf(2) eqs(int slop) l(logit) /*
*/ f(binom) weight(wt) ip(f) nip(2)
number of level 1 units = 5908
number of level 2 units = 27
Condition Number = 12.81975
gllamm model
log likelihood = -3106.6101
------------------------------------------------------------------------------
quit | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
treat | .5317816 .0666912 7.97 0.000 .4010692 .662494
_cons | -1.086669 .0919203 -11.82 0.000 -1.266829 -.9065085
------------------------------------------------------------------------------
Probabilities and locations of random effects
------------------------------------------------------------------------------
***level 2 (study)
loc1: -.53793, .35823
var(1): .19270432
loc2: -.09286, .06184
cov(2,1): .03326538
var(2): .0057424
prob: 0.3997, 0.6003
------------------------------------------------------------------------------
Add one mass at a time using gateaux derivative method (output not shown):
local n=2
while $HG_error==0&`n'<12{
matrix a = e(b)
local ll = e(ll)
local k = e(k)
local n = `n' + 1
gllamm quit treat , i(study) nrf(2) eqs(int slop) l(logit) /*
*/ f(binom) weight(wt) ip(f) nip(`n') lf0(`k' `ll') /*
*/ gateaux(-5 5 40) from(a) trace
}
Final estimates for 10 masses:
number of level 1 units = 5908
number of level 2 units = 27
Condition Number = 111.7378
gllamm model Number of obs = 5908
LR chi2(3) = 0.36
Log likelihood = -3061.5044 Prob > chi2 = 0.9488
------------------------------------------------------------------------------
quit | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
treat | .5909019 .1020571 5.79 0.000 .3908736 .7909301
_cons | -1.197405 .1530979 -7.82 0.000 -1.497471 -.8973385
------------------------------------------------------------------------------
Probabilities and locations of random effects
------------------------------------------------------------------------------
***level 2 (study)
loc1: -.17192, -1.7707, -.74877, 1.2864, .58648, -.05122, .11831, -.95241, .57538, .39284
var(1): .57783952
loc2: -.37184, -.0051, .28878, -.02044, 1.1465, .16963, -.63535, -.16783, -.13978, .05351
cov(2,1): .01816208
var(2): .09297283
prob: 0.1216, 0.106, 0.0442, 0.0461, 0.0382, 0.1482, 0.0325, 0.0355, 0.1617, 0.2662
------------------------------------------------------------------------------
Store locations and log odds as variables:
matrix a=e(zlc2)' svmat a matrix b=e(zlc3)' svmat b matrix prob = e(zps2)' svmat prob
Convert log odds to probabilities and calculate corresponding rounded percentages:
replace prob1=exp(prob1) gen percent=round(prob1*100,1)
Produce a plot similar to the upper panel of Figure 9.7:
twoway (scatter b1 a1 [w=percent], msymbol(Oh)) /* */ (scatter b1 a1, mlabel(percent) mlabpos(0) msymbol(none)), /* */ xtitle(Intercept) ytitle(Slope) legend(off) saving(blobs, replace)
Silagy, C. (2003). Nicotine replacement therapy for smoking cessation (Cochrane review). The Cochrane Library, Issue 4. Chichester: Wiley.
Rabe-Hesketh, S., Skrondal, A. and Pickles, A. (2002). Reliable estimation of generalised linear mixed models using adaptive quadrature. The Stata Journal 2, 1-21.
Skrondal, A. and Rabe-Hesketh, S. (2004). Generalized
Latent Variable Modeling: Multilevel, Longitudinal and Structural
Equation Models. Boca Raton, FL: Chapman & Hall/ CRC Press.
Outline
Datasets and do-files